ORIGIN: Starting the Conversation
Positively Stable
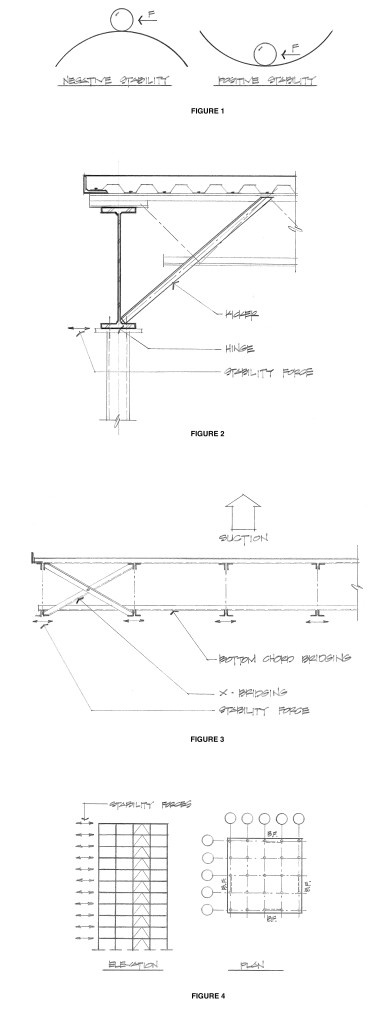 If a structural system includes an unstable element, a sudden (and possibly catastrophic) failure will eventually occur. In addition to safely resisting the applied gravity and lateral loads, a building structure should have a tendency to return to its original state when displaced. It should be positively stable.
If a structural system includes an unstable element, a sudden (and possibly catastrophic) failure will eventually occur. In addition to safely resisting the applied gravity and lateral loads, a building structure should have a tendency to return to its original state when displaced. It should be positively stable.
Both balls are at rest and adequately supported in the vertical direction. But if the ball on the left is pushed only slightly to one side, it will continue to move in the same direction and will in fact accelerate. That’s negative stability, and it’s not good when components in a structural system do that. Conversely, the ball on the right is positively stable. When it is displaced to one side, it wants to return to its original position; and the more it is displaced, the more it wants to return.
Gravity loads such as snow, occupancy, equipment, and structure self-weight – and lateral loads such as earth pressure, wind, and seismic – are typically code-prescribed and defined in the design criteria for the project. Stability forces, however, act at right angles to the applied loads, are typically associated with compression forces, and are a component of the structural system itself. They are invisible in the sense that they are not externally applied. While methods have been developed and codified to analyze some common situations such as building column and story stability, in most cases the code just stipulates that the structure must be stable and relies on the structural engineer to make it so.
Solutions to stability problems often result in members that appear to be extraneous, but they are in fact essential to the successful performance of the structural system. In the example above, a negative moment region is created in a continuous beam where it crosses over a column. The bottom flange of the beam is in compression, and as the system is loaded to capacity, the bottom flange wants to kick out to the side. The kicker is there to prevent that from happening. Despite the fact that it would be easier to connect the kicker to the bottom chord of the joist, it is connected to the top chord to satisfy another stability issue. The bottom chord is unbraced out of plane, so a connection to the bottom chord would create an unstable hinge at the connection point. The top chord is braced out of plane by the floor deck.
In the example above, the roof diaphragm is in place and connected to the roof framing members. The top chords of the joists are thus braced by the diaphragm. During high winds, however, the interior pressure exceeds the exterior pressure and the roof is sucked upward. The bottom chords of the joists go into compression and want to kick out to the side. To keep that from happening, the bottom chord bridging must be continuous and connected to each joist. Furthermore, the bridging has a stability issue of its own: due to its slenderness, it cannot take compression loads – only tension. So x-bridging is required wherever the horizontal bridging is discontinuous, and at each end of the run of bridging. Otherwise, every single joist in the bay, from one end of the building to the other, could fail simultaneously.
In the example above, every column in each story is dependent upon the lateral load-resisting system for stability. In addition to the code specified wind and seismic loads, the braced frames must resist the stability forces imparted by all of the columns. In this case, the stability forces from 25 columns must be divided between two frames in each direction.
For a classic example of negative aerodynamic stability in a bridge structure, go here.

There are no comments.